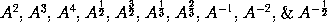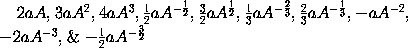Sir Isaac Newton, Philosophiae Naturalis Principia Mathematica (The Mathematical Principles of Natural Philosophy) Book Two. 3rd Edition (1726).
LEMMA II
Genitam voco quantitatem omnem, quæ ex lateribus vel terminis quibuscunque in arithmetica per multiplicationem, divisionem & extractionem radicum; in geometria per inventionem vel contentorum & laterum, vel extremarum & mediarum proportionalium, sine additione & subductione generatur. Ejusmodi quantitates sunt facti, quoti, radices, rectangula, quadrata, cubi, latera quadrata, latera cubica, & similes. Has quantitates, ut indeterminatas & instabiles, & quasi motu fluxuve perpetuo crescentes vel decrescentes, hic considero; & earum incrementa vel decrementa momentanea sum nomine momentorum intelligo: ita ut incrementa pro momentis addititiis seu affirmativis, ac decrementa pro subductitiis seu negativis habeantur. Cave tamen intellexeris particulas finitas. Particulæ finitæ non sunt momenta, sed quantitates ipsæ ex momentis genitæ. Intelligenda sunt principia jamjam nascentia finitarum magnitudinum. Neque enim spectatur in hoc lemmate magnitudo momentorum, sed prima nascentium proportio. Eodem recidit si loco momentorum usurpentur vel velocitates incrementorum ac decrementorum (quas etiam motus, mutationes & fluxiones quantitatum nominare licet) vel finitæ quævis quantitates velocitatibus hisce proportionales. Lateris autem cujusque generantis coefficiens est quantitas, quæ oritur applicando genitam ad hoc latus.
Igitur sensus lemmatis est, ut, si quantitatum quarumcunque perpetuo motu crescentium vel decrescentium A, B, C, &c. momenta, vel his proportionales mutationum velocitates dicantur a, b, c, &c. momentum vel mutatio geniti rectanguli AB fuerit aB + bA, & geniti contenti ABC momentum fuerit aBC + bAC + cAB: & genitarum dignitatum
momenta
respective. Et generaliter, ut dignitatis cujuscunque 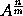 momentum fuerit
momentum fuerit 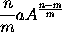 Item ut genitæ A²B momentum fuerit 2aAB + bA²; & genitæ
Item ut genitæ A²B momentum fuerit 2aAB + bA²; & genitæ 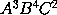 momentum
momentum 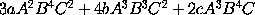 ; & genitæ
; & genitæ 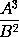 sive
sive 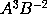 momentum
momentum 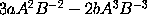 : & sic in cæteris. Demonstrantur vero lemma in hunc modum.
: & sic in cæteris. Demonstrantur vero lemma in hunc modum.
Cas. 1. Rectangulum quodvis motu perpetuo auctum AB ubi de lateribus A & B deerant momentorum dimidia 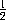 a &
a & 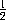 b, fuit A –
b, fuit A – 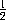 a in B –
a in B – 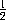 b, seu AB –
b, seu AB – 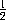 aB –
aB – 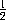 Ba +
Ba + 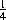 ab; & quam primum latera A & B alteris momentorum dimidiis aucta sunt, evadit A +
ab; & quam primum latera A & B alteris momentorum dimidiis aucta sunt, evadit A + 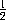 a in B +
a in B + 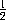 b, seu AB +
b, seu AB + 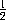 aB +
aB + 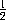 Ba +
Ba + 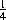 ab. De hoc rectangulo subducator rectangulum prius, & manebit excessus aB + bA. Igitur laterum incrementis totis a & b generatur rectanguli incrementum aB + bA. Q.E.D.
ab. De hoc rectangulo subducator rectangulum prius, & manebit excessus aB + bA. Igitur laterum incrementis totis a & b generatur rectanguli incrementum aB + bA. Q.E.D.
Cas. 2. Ponatur AB semper æquale G, & contenti ABC seu GC momentum (per cas. 1.) erit gC + cG, id est (si pro G & g scribantur AB & aB + bA) aBC + bAC + cAB. Et par est ratio contenti sub lateribus quotcunque. Q.E.D.
Cas. 3. Ponantur latera A, B, C sibi mutuo semper æqualia; & ipsius A², id est rectanguli AB, momentum aB + bA erit 2aA, ipsius autem A³, id est contenti ABC, momentum aBC + bAC + cAB erit 3aA². Et eodem argumento momentum dignitatis cujuscunque 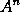 est
est 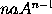 . Q.E.D.
. Q.E.D.
Cas. 4. Unde cum 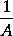 in A sit 1, momentum ipsius
in A sit 1, momentum ipsius 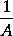 ductum in A, una cum
ductum in A, una cum 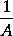 ducto in a erit momentum ipsius 1, id est, nihil. Proinde momentum ipsius
ducto in a erit momentum ipsius 1, id est, nihil. Proinde momentum ipsius 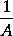 seu ipsius
seu ipsius 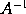 est
est 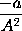 . Et generaliter cum
. Et generaliter cum 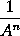 in
in 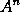 sit 1, momentum ipsius
sit 1, momentum ipsius 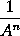 ductum in
ductum in 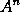 una cum
una cum 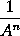 in
in 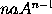 erit nihil. Et propterea momentum ipsius
erit nihil. Et propterea momentum ipsius 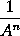 seu
seu 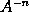 erit
erit 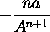 . Q.E.D.
. Q.E.D.
Cas. 5. Et cum 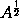 in
in 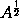 sit A, momentum ipsius
sit A, momentum ipsius 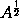 ductum in 2
ductum in 2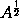 erit a, per cas. 3: ideoque momentum ipsius
erit a, per cas. 3: ideoque momentum ipsius 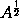 erit
erit 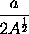 sive
sive 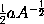 . Et generaliter si ponatur
. Et generaliter si ponatur 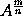 æquale B, erit
æquale B, erit 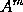 æquale
æquale 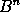 , ideoque
, ideoque 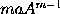 æquale
æquale 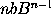 , &
, & 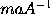 æquale
æquale 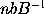 seu
seu 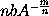 , ideoque
, ideoque 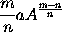 æquale b, id est, momento ipsius
æquale b, id est, momento ipsius 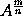 . Q.E.D.
. Q.E.D.
Cas. 6. Igitur genitæ cujuscunque 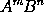 momentum est momentum ipsius
momentum est momentum ipsius 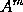 ductum in
ductum in 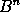 , una cum momento ipsius
, una cum momento ipsius 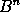 ducto in
ducto in 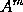 , id est
, id est 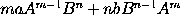 ; idque sive dignitatum indices m & n sint integri numeri vel fracti, sivi affirmativi vel negativi. Et par est ratio contenti sub pluribus dignitatibus. Q.E.D.
; idque sive dignitatum indices m & n sint integri numeri vel fracti, sivi affirmativi vel negativi. Et par est ratio contenti sub pluribus dignitatibus. Q.E.D.
Corol. 1 Hinc in continue proportionalibus, si terminus unus datur, momenta terminorum reliquorum erunt ut iidem termini multiplicati per numerum intervallorum inter ipsos & terminum datum. Sunto A, B, C, D, E, Fcontinue proportionales; & si detur terminus C, momenta reliquorum terminorum erunt inter se ut -2A, –B, D, 2E, 3F.
Corol. 2 Et si in quatuor proportionalibus duæ mediæ dentur, momenta extremarum erunt ut eædem extremæ. Idem intelligendum est de lateribus rectanguli cujuscunque dati.
Corol. 3. Et si summa vel differentia duorum quadratorum detur, momenta laterum erunt reciproce ut latera.
Scholium
Links:
D.R. Wilkins (dwilkins@maths.tcd.ie) School of Mathematics Trinity College, Dublin