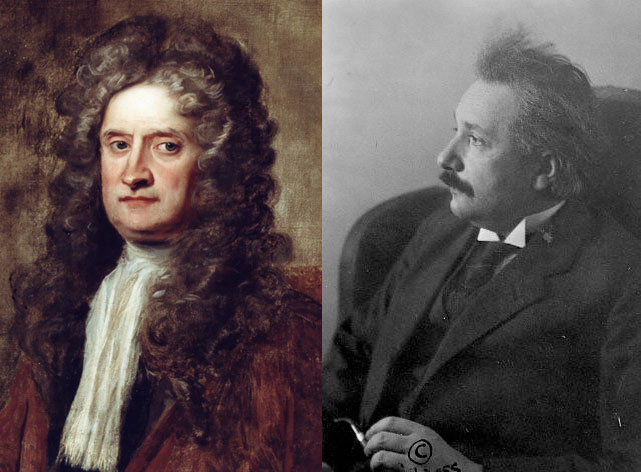
In his eulogy to Isaac Newton written in 1927, the bicentenary of the great man’s death, Einstein called him a “shining spirit.” Enlarge Photo credit: Courtesy The Royal Society, www.royalsoc.ac.uk and © CORBIS
By Albert Einstein
He was not only an inventor of genius in respect of particular guiding methods; he also showed a unique mastery of the empirical material known in his time, and he was marvelously inventive in special mathematical and physical demonstrations. For all these reasons he deserves our deep veneration. He is, however, a yet more significant figure than his own mastery makes him, since he was placed by fate at a turning point in the world’s intellectual development. This is brought home vividly to us when we recall that before Newton there was no comprehensive system of physical causality which could in any way render the deeper characters of the world of concrete experience.
The great materialists of ancient Greek civilization had indeed postulated the reference of all material phenomena to a process of atomic movements controlled by rigid laws, without appealing to the will of living creatures as an independent cause. Descartes, in his own fashion, had revived this ultimate conception. But it remained a bold postulate, the problematic ideal of a school of philosophy. In the way of actual justification of our confidence in the existence of an entirely physical causality, virtually nothing had been achieved before Newton.
Newton’s aim
Newton’s aim was to find an answer to the question: Does there exist a simple rule by which the motion of the heavenly bodies of our planetary system can be completely calculated, if the state of motion of all these bodies at a single moment is known? Kepler’s empirical laws of the motion of the planets, based on Tycho Brahe’s observations, were already enunciated, and demanded an interpretation.* These laws gave a complete answer to the question of how the planets moved round the sun (elliptical orbit, equal areas described by the radius vector in equal periods, relation between semi-major axis and period of revolution). But these rules do not satisfy the requirement of causality. The three rules are logically independent of one another, and show no sign of any interconnection. The third law cannot be extended numerically as it stands, from the sun to another central body; there is, for instance, no relation between a planet’s period of revolution round the sun and the period of revolution of a moon round its planet.
The German mathematician and astronomer Johannes Kepler, in his famous laws of planetary motion, showed how the planets are held in their orbits, but he could not explain why. That task was left to the young Isaac Newton. (Photo credit: Courtesy The MacTutor History of Mathematics archive, University of St. Andrews)
But the principal thing is that these laws have reference to motion as a whole, and not to the question of how there is developed from one condition of motion of a system that which immediately follows it in time. They are, in our phraseology of today, integral laws and not differential laws.
It was, no doubt, especially impressive to learn that the cause of the movements of the heavenly bodies is identical with the force of gravity so familiar to us from everyday experience.
The differential law is the form which alone entirely satisfies the modern physicist’s requirement of causality. The clear conception of the differential law is one of the greatest of Newton’s intellectual achievements. What was needed was not only the idea but a formal mathematical method which was, indeed, extant in rudiment but had still to gain a systemic shape. This also Newton found in the differential and integral calculus. It is unnecessary to consider whether Leibniz arrived at these same mathematical methods independently of Newton or not; in any case, their development was a necessity for Newton, as they were required in order to give Newton the means of expressing his thought.
From Galileo to Newton
Galileo had already made a significant first step in the recognition of the law of motion. He discovered the law of inertia and the law of free falling in the Earth’s field of gravitation: A mass (or, more accurately, a material point) uninfluenced by other masses moves uniformly in a straight line; the vertical velocity of a free body increases in the field of gravity in proportion to the time. It may seem to us today to be only a small step from Galileo’s observations to Newton’s laws of motion. But it has to be observed that the two propositions above, in the form in which they are given, relate to motion as a whole, while Newton’s law of motion gives an answer to the question: How does the condition of motion of a point-mass change in an infinitely small period under the influence of an external force? Only after proceeding to consider the phenomenon during an infinitely short period (differential law) does Newton arrive at a formula which is applicable to all motions. He takes the conception of force from the already highly developed theory of statics. He is only able to connect force with acceleration by introducing the new conception of mass, which, indeed, is supported curiously enough by an apparent definition. Today we are so accustomed to forming conceptions which correspond to differential quotients that we can hardly realize any longer how great a capacity for abstraction was needed to pass across a double barrier to the general differential laws of motion, with the further need to evolve the conception of mass.
Galileo, seen here showing his telescope to the Doge of Venice, set the stage for Newton’s formulation of his three laws of motion. (Photo credit: © Scala/Art Resource, NY)
But this was still a long way from the causal comprehension of the phenomena of motion. For the motion was only determined by the equation of motion if the force was given. Newton had the idea, to which he was probably led by the laws of the planetary motions, that the force acting on a mass is determined by the position of all masses at a sufficiently small distance from the mass in question. Not until this connection was realized was a completely causal comprehension of the phenomena of motion obtained. How Newton, proceeding from Kepler’s laws of the motion of planets, solved this problem for gravitation and so discovered the identity of the nature of gravity with the motive forces acting on the stars is common knowledge. It is only the combination of—
(Law of motion) + (Law of attraction)
through which is constituted that wonderful thought-structure which enables the earlier and later conditions of a system to be calculated from the conditions ruling at one particular time, insofar as the phenomena occur under the sole influence of the forces of gravitation. The logical completeness of Newton’s system of ideas lay in the fact that the sole causes of the acceleration of the masses of a system prove to be the masses themselves.
Newton’s theory of motion suffered its first shock from Maxwell’s theory of electricity.
On the basis sketched Newton succeeded in explaining the motions of the planets, moons, comets, down to fine details as well as the ebb and flow of the tides and the precessional movement of the Earth—this last a deductive achievement of particular brilliance. It was, no doubt, especially impressive to learn that the cause of the movements of the heavenly bodies is identical with the force of gravity so familiar to us from everyday experience.
Newton succeeded in describing the movements of the planets, moons, and comets to an extraordinarily fine degree. (Photo credit: © NOVA/WGBH Educational Foundation)
Significance of Newton’s achievement
The significance, however, of Newton’s achievement lay not only in its provision of a serviceable and logically satisfactory basis for mechanics proper; up to the end of the 19th century it formed the program of all theoretical research. All physical phenomena were to be referred to as masses subject to Newton’s law of motion. Only the law of force had to be amplified and adapted to the type of phenomena which were being considered. Newton himself tried to apply the program in optics, on the hypothesis that light consisted of inert corpuscles. The optics of the undulatory theory also made use of Newton’s law of motion, the law being applied to continuously diffused masses. The kinetic theory of heat rested solely on Newton’s formulae of motion; and this theory not only prepared people’s minds for recognition of the law of the conservation of energy, but also supplied a theory of gases confirmed in its smallest details, and a deepened conception of the nature of the second law of thermodynamics. The theory of electricity and magnetism also developed down to modern times entirely under the guidance of Newton’s basic ideas (electric and magnetic substance, forces at a distance). Even Faraday and Maxwell’s revolution in electrodynamics and optics, which was the first great advance in the fundamental principles of theoretical physics since Newton, was still achieved entirely under the guidance of Newton’s ideas. Maxwell, Boltzmann, and Lord Kelvin never tired of trying again and again to reduce electromagnetic fields and their dynamical reciprocal action to mechanical processes occurring in continuously distributed hypothetical masses. But owing to the barrenness, or at least the unfruitfulness, of these efforts there gradually occurred, after the end of the 19th century, a revulsion in fundamental conceptions; theoretical physics outgrew Newton’s framework, which had for nearly two centuries provided fixity and intellectual guidance for science.
The work of Michael Faraday (left) and James Clerk Maxwell on electrodynamics was, says Einstein, “the first great advance in the fundamental principles of theoretical physics since Newton…” (Photo credit: Courtesy The MacTutor History of Mathematics archive, University of St. Andrews and © Bettmann/CORBIS)
Newton on its limitations
Newton’s basic principles were so satisfying from a logical standpoint that the impulse to fresh departures could only come from the pressure of the facts of experience. Before I enter into this I must emphasize that Newton himself was better aware of the weak sides of his thought-structure than the succeeding generations of students. This fact has always excited my reverent admiration; I should like, therefore, to dwell a little on it.
- Although everyone has remarked how Newton strove to represent his thought-system as necessarily subject to the confirmation of experience, and to introduce the minimum of conceptions not directly referable to matters of experience, he makes use of the conceptions of absolute space and absolute time. In our own day he has often been criticized for this. But it is in this very point that Newton is particularly consistent. He had recognized that the observable geometrical magnitudes (distances of material points from one another) and their change in process of time do not completely determine movements in a physical sense. He shows this in the famous bucket experiment. There is, therefore, in addition to masses and their distances, varying with time, something else, which determines what happens; this “something” he conceives as the relation to “absolute space.” He recognizes that space must possess a sort of physical reality if his laws of motion are to have a meaning, a reality of the same sort as the material points and their distances.This clear recognition shows both Newton’s wisdom and a weak side of his theory. For a logical construction of the theory would certainly be more satisfactory without this shadowy conception; only those objects (point-masses, distances) would then come into the laws whose relation to our perceptions is perfectly clear.
- The introduction of direct instantaneously acting forces at a distance into the exposition of the effects of gravitation does not correspond to the character of most of the phenomena which are familiar to us in our daily experience. Newton meets this objection by pointing out that his law of reciprocal gravitation is not to be taken as an ultimate explanation, but as a rule induced from experience.
- Newton’s theory offered no explanation of the very remarkable fact that the weight and inertia of a body are determined by the same magnitude (the mass). The remarkable nature of this fact struck Newton also.
None of these three points can rank as a logical objection against the theory. They form, as it were, merely unsatisfied needs of the scientific spirit in its effort to penetrate the processes of nature by a complete and unified set of ideas.
The theory of the electromagnetic field
Newton’s theory of motion, considered as a program for the whole field of theoretical physics, suffered its first shock from Maxwell’s theory of electricity. It was found that the reciprocal action between bodies through electrical and magnetic bodies does not take place through instantaneously acting forces at a distance, but through processes which are transmitted with finite velocity through space. Alongside the point-mass and its movements there arose, in Faraday’s conception, a new sort of physically real thing, the “field.” It was first sought to conceive this, with the aid of mechanical modes of thought, as a mechanical condition (of movement or strain) of a hypothetical space-filling medium (the ether). When, however, in spite of the most obstinate efforts, this mechanical interpretation refused to work, students slowly accustomed themselves to the conception of the “electromagnetic field” as the ultimate irreducible foundation stone of physical reality. We owe to [Heinrich] Hertz the deliberate liberation of the conception of the field from all the scaffolding of the conceptions of mechanics, and to [Hendrik Antoon] Lorentz the liberation of the conception of the field from a material bearer; according to Lorentz the physical empty space (or ether) alone figured as bearer of the field; in Newton’s mechanics, indeed, space had not been devoid of all physical functions. When this development had been completed, no one any longer believed in directly acting instantaneous forces at a distance, even in connection with gravitation, though a field theory for gravitation, for lack of sufficient known facts, was not unmistakably indicated. The development of the theory of the electromagnetic field also led, after Newton’s hypothesis of action at a distance had been abandoned, to the attempt to find an electromagnetic explanation for Newton’s law of motion, or to replace that law by a more accurate law based on the field theory. These efforts were not crowned with full success, but the mechanical basic conceptions ceased to be regarded as foundation stones of the physical conception of the universe.
The Maxwell-Lorentz theory led inevitably to the special theory of relativity, which, by destroying the conception of absolute simultaneity, negatived the existence of forces at a distance. Under this theory mass is not an unalterable magnitude, but a magnitude dependent on (and, indeed, identical with) the amount of energy. The theory also showed that Newton’s law of motion can only be considered as a limiting law valid only for small velocities, and substituted for it a new law of motion, in which the velocity of light in a vacuum appears as the limiting velocity.
The general theory of relativity
The last step in the development of the program of the field theory was the general theory of relativity. Quantitatively it made little modification in Newton’s theory, but qualitatively a deep-seated one. Inertia, gravitation, and the metrical behavior of bodies and clocks were reduced to the single quality of a field, and this field in turn was made dependent on the bodies (generalization of Newton’s law of gravitation or of the corresponding field law, as formulated by Siméon Denis Poisson). Space and time were so divested, not of their reality, but of their causal absoluteness (absoluteness-influencing, that is, not -influenced), which Newton was compelled to attribute to them in order to be able to give expression to the laws then known. The generalized law of inertia takes over the role of Newton’s law of motion. From this short characterization it will be clear how the elements of Newton’s theory passed over into the general theory of relativity, the three defects above mentioned being at the same time overcome. It appears that within the framework of the general theory of relativity the law of motion can be deduced from the law of the field, which corresponds to Newton’s law of force.
The whole development of our ideas concerning natural phenomena may be conceived as an organic development of Newton’s thought.
Newton’s mechanics prepared the way for the theory of fields in a yet more formal sense. The application of Newton’s mechanics to continuously distributed masses led necessarily to the discovery and application of partial differential equations, which in turn supplied the language in which alone the laws of the theory of fields could be expressed. In this formal connection also Newton’s conception of the differential law forms the first decisive step to the subsequent development.
The whole development of our ideas concerning natural phenomena, which has been described above, may be conceived as an organic development of Newton’s thought. But while the construction of the theory of fields was still actively in progress, the facts of heat radiation, spectra, radioactivity, and so on revealed a limit to the employment of the whole system of thought, which, in spite of gigantic successes in detail, seems to us today completely insurmountable. Many physicists maintain, not without weighty arguments, that in face of these facts not only the differential law but the law of causality itself—hitherto the ultimate basic postulate of all natural science—fails.
The very possibility of a spatio-temporal construction which can be clearly brought into consonance with physical experience is denied. That a mechanical system should permanently admit only discrete values of energy or discrete states—as experience, so to say, directly shows—seems at first hardly deducible from a theory of fields working with differential equations. The method of [Louis] De Broglie and [Erwin] Schrödinger, which has, in a certain sense, the character of a theory of fields, does deduce, on the basis of differential equations, from a sort of consideration of resonance the existence of purely discrete states and their transition into one another in amazing agreement with the facts of experience; but it has to dispense with a localization of the mass-particles and with strictly causal laws. Who would be so venturesome as to decide today the question whether causal law and differential law, these ultimate premises of Newton’s treatment of nature, must definitely be abandoned?
*Everyone knows today what gigantic efforts were needed to discover these laws from the empirically ascertained orbits of the planets. But few reflect on the genius of the method by which Kepler ascertained the true orbits from the apparent ones, i.e., their directions as observed from the Earth.
Editor’s note: This article appeared in the Smithsonian Annual Report for 1927, the second centenary of Newton’s death. It’s somewhat dense, but then, what do you expect from the greatest scientist who ever lived talking about the accomplishments of the other greatest scientist who ever lived?
Article Source: pbs
No comments yet.