Isaac Newton’s Principia – Summary & Preface

Introduction and Summary

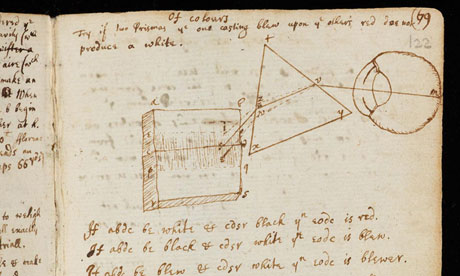
Original manuscript by Sir Isaac Newton, one of several by the English physicist to be made available on the web. Photograph: Cambridge University Library/PA

The Principia, arguably the most important book published in modern European history, began by offering the reader three basic principles, which have come to be known as Newton’s three laws of motion:

• 1. Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.
• 2. The change in motion is proportional to the motive force impressed, and is made in the direction of the straight line in which that force is impressed.
• 3. To every action there is always opposed an equal reaction. Even today, these three laws are the basic axioms on which physics rests, and the first principles that every high school physics student learns.

From this opening, Newton proceeded to the meat of his book, the principle of gravitation and its role in the solar system. He showed how his inverse square law worked perfectly with Kepler’s elliptical orbits; how planets are deflected into orbit around the sun by the pull of the sun’s gravity, and how the same principle can be used to explain the orbit of the moon and of Jupiter’s moons; he demonstrated that Descartes’ theory of vortices lacked the same explanatory power. Working from Halley’s research on the subject, he declared that comets transcribed orbits around the sun just as planets did; he calculated the mass of each planet; he used the pull of the sun’s gravity to account for the flattening of the Earth at the poles and the bulge at the equator; he used the gravitational pull of the moon and sun to explain the ocean tides. In his account, the entire universe was held together in a web of gravitational pulls, acting on every star, planet, moon and comet; thus Newton rendered the whole universe explainable by a law–subject to the insight of mathematics and the human mind.

Quotes from Isaac Newton’s Principia Mathematica

…from the same principles, I now demonstrate the frame of the System of the World.

Hypotheses non fingo. I feign no hypotheses.

The description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn.

I will not define time, space, place and motion, as being well known to all.

Geometry does not teach us to draw these lines, but requires them to be drawn; for it requires that the learner should first be taught to describe these accurately, before he enters upon geometry; then it shows how by these operations problems may be solved.

We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances.

I have not as yet been able to discover the reason for these properties of gravity from phenomena, and I do not feign hypotheses.

Preface to Isaac Newton’s Principia

Since the ancients esteemed the science of mechanics of greatest importance in the investigation of natural things, and the moderns, rejecting substantial forms and occult qualities, have endeavoured to subject the phenomena of nature to the laws of mathematics, I have in this treatise cultivated mathematics as far as it relates to natural philosophy. The ancients considered mechanics in a twofold respect; as rational, which proceeds accurately by demonstration, and practical. To practical mechanics all the manual arts belong, from which mechanics took its name. But as artificers do not work with perfect accuracy, it comes to pass that mechanics is so distinguished from geometry that what is perfectly accurate is called geometrical; what is less so, is called mechanical. However, the errors are not in the art, but in the artificers. He that works with less accuracy is an imperfect mechanic; and if any could work with perfect accuracy he would be the most perfect mechanic of all. …

I consider natural philosophy rather than arts and write not concerning manual but natural powers, and consider chiefly those things which relate to gravity, levity, elastic force, the resistance of fluids, and the like forces, whether attractive or impulsive; and therefore I offer this work as the mathematical principles of natural philosophy, for the whole burden of philosophy seems to consist in this – from the phenomena of motions to investigate the forces of nature, and then from these forces to demonstrate the other phenomena. …

I wish we could derive … the phenomena of Nature … from mechanical principles, for I am induced by many reasons to suspect that they all may depend upon certain forces by which the particles of bodies, by some causes hitherto unknown, are either mutually impelled towards one another, and cohere in regular figures, or are repelled and recede from one another. These forces being unknown, philosophers have hitherto attempted the search of Nature in vain; but I hope the principles here laid down will afford some light either to this or some truer method of natural philosophy.